To czym są te liczby binarne?
Zastanawiałeś się kiedyś w jaki sposób działają urządzenia cyfrowe? Jak to jest, że w tak szybki sposób przetwarzają ogromne ilości danych? A może jesteś uczniem lub studentem i potrzebujesz wiedzy czym są liczby binarne, jak je zamieniać oraz jak wykonywać na nich działania matematyczne, bo kolokwium lub egzamin już lada moment?
Każdy znajdzie tutaj coś dla siebie. Zapraszam! 🙂
Każda czynność wykonywana, np. na naszym komputerze tłumaczona jest na tak zwany ciąg liczb binarnych. My, ludzie, przywykliśmy do operowania na liczbach dziesiętnych ale dla urządzeń byłoby to zbyt duże obciążenie, w rezultacie niewydajne rozwiązanie.
Choć w naszej codzienności nie operujemy na liczbach binarnych, to niewątpliwie w informatyce pojawiają się bardzo często. Oznaczają bardzo prostą reprezentację dowolnej informacji w formie wielu cyfr 0 oraz 1, w rezultacie tworząc ciąg.
Dlaczego informatyka tak „lubi” liczby binarne?
Ponieważ taka forma jest bardzo prosta! Dwie cyfry pozwalają uzyskać stany: włączony lub wyłączony / prawda lub fałsz / 0 lub 1. Dzięki minimalizacji stanów, ograniczone zostaje ryzyko niedokładności wyliczeń. Co więcej, na takiej formie danych bazują mózgi naszych urządzeń, czyli procesory, które są zbudowane z tranzystorów. To właśnie tranzystory panują nad wszystkimi informacjami, poprzez sterowanie prądem, który płynie (1) lub nie (0). O procesorach i tranzystorach zrobimy sobie osobny artykuł.
Liczby binarne na dziesiętne i odwrotnie
Indeksy
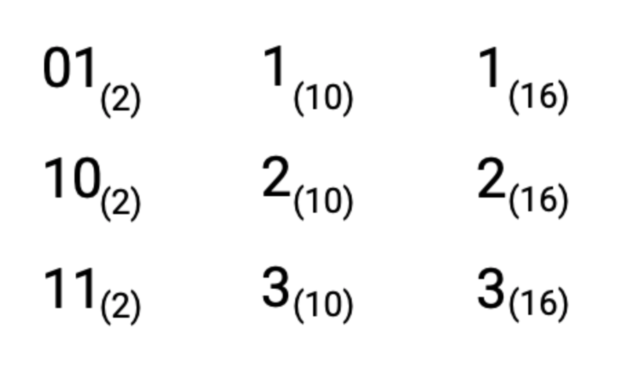
Skąd mam wiedzieć, że liczba należy do dziesiętnych, czy jednak jest wartością binarną?
Zwracaj uwagę na to co znajduje się za ostatnią cyfrą wartości. Jest to tzw. indeks, który posiada informację w jakim systemie jest zapisana liczba, np. 2 (binarny), 10 (dziesiętny), 16 (szesnastkowy).
Dziesiętne na binarne
No dobrze, komputery „nauczyły się” zamieniać liczby dziesiętne na binarne, ale skąd ja mam wiedzieć jak to zrobić?
Wyliczyć! Nie jest to takie trudne jak mogłoby się wydawać. Zobacz:
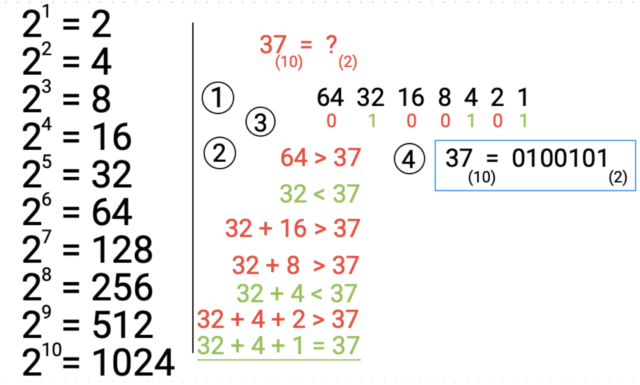
Po lewej części powyższego obrazka jest pierwszych dziesięć potęg liczby dwa. Nie ma sensu wypisywać więcej, ale tych kilka warto mieć pod ręką na potrzeby zadania. Dlaczego interesują nas potęgi dwójki? Ponieważ liczba 2 jest podstawą systemu dwójkowego.
Po prawej stronie zdjęcia umieszczone jest proste zadanie. Należy wyliczyć wartość binarną z liczby 37. Dla ułatwienia umieściłem punkty oznaczające kolejność działań:
- Wypisuj kolejne wartości potęg od prawej do lewej, do momentu aż uzyskasz wartość potęgi liczby 2, większą od wyliczanej. W moim przypadku szukaną jest 37, więc pierwszą, większą wartością potęgi będzie 64.
- Wartości potęg bierz po kolei, od lewej do prawej i sprawdzaj czy jest mniejsza, czy większa od naszej liczby 37. Interesują nas tylko te mniejsze. Większe wartości oznaczaj, np. kolorem czerwonym – przyda się to w kroku 3. Jeżeli znalazłeś liczbę mniejszą, do kolejnego równania musisz wziąć tę znalezioną + aktualną. W naszym przypadku pierwszą znalezioną była 32 (oznaczona na zielono) dlatego do niej dodajemy aktualną 16. Działamy w ten sposób do momentu znalezienia liczby równej naszej szukanej.
- Ten krok sprawdza, w których miejscach równania są oznaczone na czerwono. Liczbę z czerwonego równania odnajdź na liście z pierwszego kroku i wpisz 0, w pozostałych 1.
Uwaga: Jeżeli równanie przy którym znalazłeś szukaną wartość stanęło, np. na wartości potęgi równej 4, to pod kolejnymi wartościami (2 oraz 1) wpisz 0.
- Ten punkt to już ostateczna odpowiedź do zadania 🙂 Proste, prawda?
Binarne na dziesiętne
A w drugą stronę się da?
No jasne i jest to jeszcze łatwiejsze! Zerknij poniżej:

- W pierwszym kroku ponownie rozpisz, od prawej do lewej, kolejne wartości potęg liczby 2. Interesuje Cię tyle liczb ile jest cyfr w ciągu binarnym.
- Teraz przepisz ciąg binarny i dopasuj każdą cyfrę do wartości potęg. Dla ułatwienia cyfry 0 możesz oznaczyć, np. na czerwono
- Namierz cyfry 1 w przepisanym ciągu i zsumuj liczby znajdujące się nad nimi.
- Odpowiedź do zadania 🙂
Dodawanie, odejmowanie, mnożenie, dzielenie liczb binarnych
Podobnie jak na liczbach dziesiętnych, na liczbach binarnych również wykonujemy działania matematyczne. Bazują na bardzo podobnych zasadach.
Dodawanie
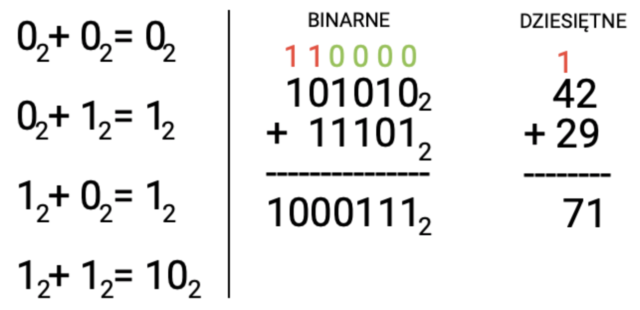
Jak możesz zauważyć, po lewej stronie umieściłem tzw. tabliczkę dodawania liczb binarnych. Są to reguły, które powinieneś stosować przy obliczeniach w „słupku” (taka legalna ściąga).
Obliczenia wykonuje się analogicznie jak w przypadku liczb dziesiętnych. Dodawanie rozpocznij od prawej do lewej strony. Więc tak:
- 0 + 1, zerknij do tabliczki. Tak jest, wynik to 1, możesz zapisać.
- 1 + 0, rzut oka na tabliczkę… 1! Zapisz i idziemy dalej.
- 0 + 1, już było więc to łatwizna 😉
- 1 + 1, o i tu ciekawy przypadek! Zgodnie z tabliczką dodawania, wynik to 10. 0 zapisz pod kreską, a 1 przenieś do kolejnej kolumny po lewej. Zauważ, że wcześniej nie zapisywałeś podobnych wartości, umieść w tych miejscach 0 (zaznaczone na zielono).
- 0 + 1, już było ale uważaj! Pamiętaj, że masz jedną 1 przeniesioną, tak więc 0 + 1 = 1 ale następnie musisz zrobić 1 + 1, a to już daje 10. Z tą wartością zrób podobnie jak w kroku numer 4.
- Teraz masz 1 i 1 przeniesioną z poprzedniego kroku, zsumuj je. Dzięki temu, że nie ma żadnej liczby dalej, możesz bez przeszkód zapisać wartość 10.
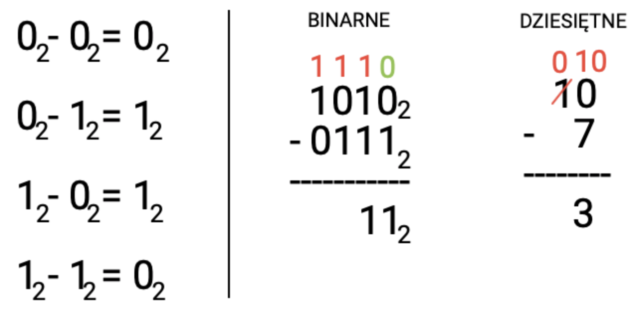
Odejmowanie
W odejmowaniu nie jest tak łatwo. Jest kilka rzeczy, o których należy pamiętać. Pułapka czycha już w tabliczce odejmowania, w drugim wierszu. 0 – 1 rzeczywiście daje 1 ale trzeba pamiętać o pożyczce z wartości wyższej wagi, przykład lepiej to wyjaśni.
- 0 – 1, zgodnie z tabliczką daje to 1 ale jest tu pułapka, o której wspominałem. Wpisz 1 pod kreską wynikową i zapisz wartość pożyczoną nad drugą kolumną.
- Teraz jest 1 – 1, łatwizna… 0? Pamiętaj, że masz pożyczkę z wartością 1. Musisz teraz zrobić 0 – 1 (pożyczka), co ponownie generuje pożyczkę z kolejnej kolumny.
- W trzeciej kolumnie jest 0 – 1 co daje wynik 1. Pamiętaj o pożyczce nad kolumną! Zrób teraz 1 – 1, czego wynikiem będzie 0.
- Ostatnia kolumna to 1 – 0, czyli 1. Z pamięci wyciągnij pożyczoną 1 i mamy 1 – 1. W rezultacie otrzymujesz 0.
- Nieznaczące 0 po lewej stronie wyniku można skreślić i otrzymujesz wartość 11.
Pamiętasz jak mówiłem o pułapkach? Co się dzieje gdy w przypadku liczb dziesiętnych od mniejszej liczby odejmiesz większą? Dostaniesz wynik na minusie. W przypadku liczb binarnych takiej sytuacji nie ma i występuje stan niedomiaru.
Jest to sytuacja, w której zapętlamy się w pożyczaniu 1 od „sąsiada” po lewej stronie. W związku z tym wpadliśmy w sytuację, gdzie moglibyśmy zapożyczać się w nieskończoność, a taki wynik jest niepoprawny. Przykład poniżej.
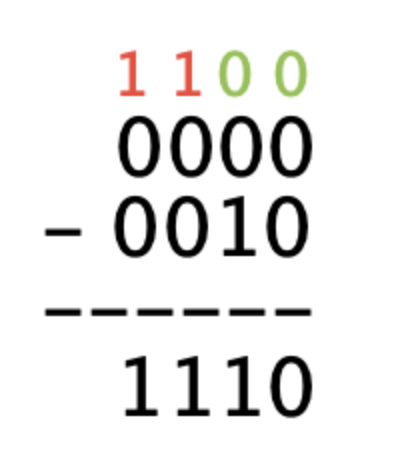
Od liczby 0 chcemy odjąć liczbę 2. Przy drugiej kolumnie zaczyna się pierwsza pożyczka i cięgnie się w nieskończoność.
Mnożenie
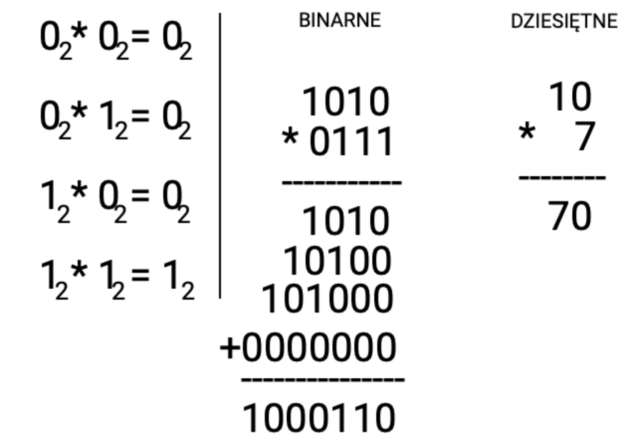
Jeżeli przeszedłeś przez dodawanie i odejmowanie, to mnożenie nie sprawi Ci problemu.
- Tak samo jak w mnożeniu liczb dziesiętnych, każda liczba mnożnej (górny wiersz) musi zostać przemnożona przez każdą liczbę mnożnika (dolny wiersz).
- Każda liczba mnożnika ma swój własny wiersz, tzw. iloczyn częściowy. Wyniki zapisuj w linii prostej pod aktualnym mnożnikiem, a puste miejsca po prawej stronie uzupełnij bitami 0.
- Po przemnożeniu wszystkich liczb, zsumuj wiersze per kolumny stosując zasady dodawania liczb binarnych.
Dzielenie
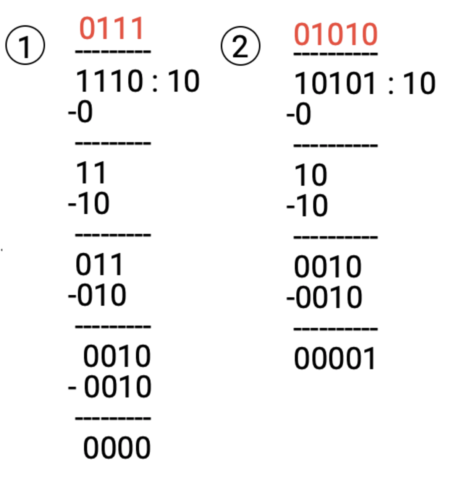
Dzielenie również jest bardzo podobne, do tego które znasz z czasów szkoły. Tutaj nie ma specjalnej tabliczki dzielenia i realizuje się je etapami.
- Sprawdzaj czy dzielnik (liczba po prawej) mieści się w liczbach dzielnej (po lewej) i zapisuj wynik na samej górze (zaznaczone na czerwono).
- Do porównań bierz pojedynczo każdy bit z dzielnej.
- Jeżeli dzielnik mieści się, odejmij go od liczb z dzielnej. Jeżeli nie, to wpisz nad kreską wynikową 0, dobierz kolejny bit i ponownie porównaj.
- Wartości odejmujesz od siebie zgodnie z tabliczką odejmowania liczb binarnych.
- Powtarzaj te czynności do momentu aż wszystkie bity się wyzerują.
- Jeżeli dojdziesz do sytuacji, w której bit lub ciąg bitów jest mniejszy od dzielnika (tak jak w przypadku ostatniego etapu z przykładu numer 2) i nie możesz dobrać kolejnego, wówczas pozostałość określ jako reszta z dzielenia.
Dotarłeś do końca!
To już koniec tego artykułu. Sporo tego wyszło ale mam nadzieję, że wiesz już o co w tym wszystkim chodzi i możesz biegle działać na liczbach binarnych. Jeśli jednak coś nie jest jeszcze w pełni jasne, napisz komentarz, postaram się odpowiedzieć i pomóc!
Jeżeli chcesz być na bieżąco z artykułami i jesteś ciekawy co będzie dalej, zapisz się do newslettera i daj lajka na naszym profilu FB!
Dzięki za Twój czas, widzimy się niebawem 🙂